The Oberth Effect

Why going down first helps you go higher.

Second stage of the launch of the James Webb Space Telescope (JWST) taking advantage of the Oberth effecthttps://www.youtube.com/watch?v=7nT7JGZMbtM&ab_channel=NASA.

Maths

The Oberth effect maximises the efficiency of a rocket burn by considering the instantaneous kinetic energy of the rocket at particular moments during its flight and selecting the most suitable time to burn. This concept can be understood by analysing the equation for the kinetic energy of a body at a given instantaneous moment.

\[\Delta KE = {1/2} m v^2\]

Now, the change in kinetic energy between two instantaneous moments (e.g., from beginning to the end of a burn) can be expressed.

\[\Delta KE = {KE}_2 - {KE}_1\]

Also assuming that the change in mass of the craft is negligible (i.e., \({m_1} \approx {m_2} \approx m\))

\[\Delta KE = {1/2} m ( {v_2}^2 - {v_1}^2 )\]

Now, taking the value \({1/2} m\) as an arbitrary scalar, the function above can be graphed in 3D as shown belowhttps://www.math3d.org/.

Three dimensional graph of the change in kinetic energy with respect to the speed of the object before and after an engine burn.

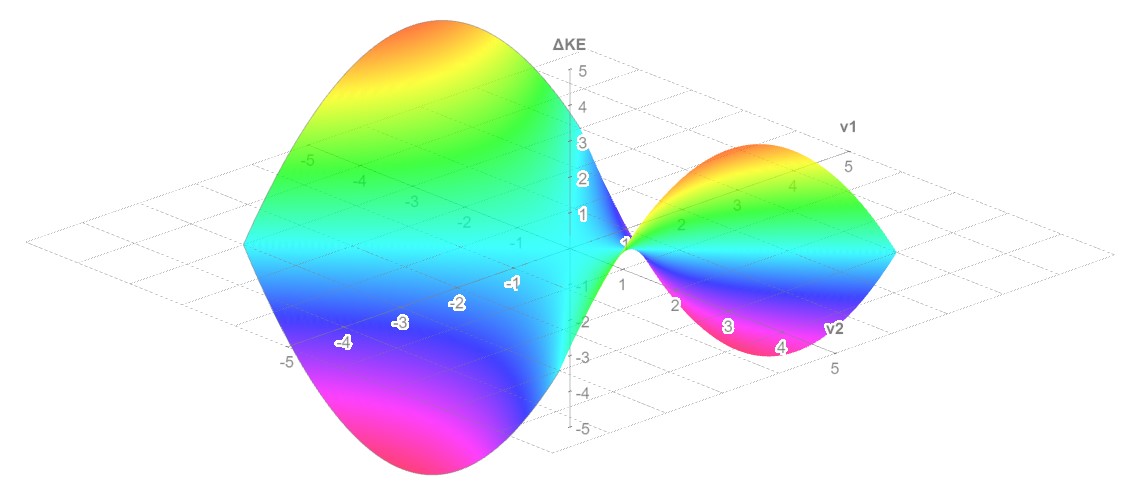
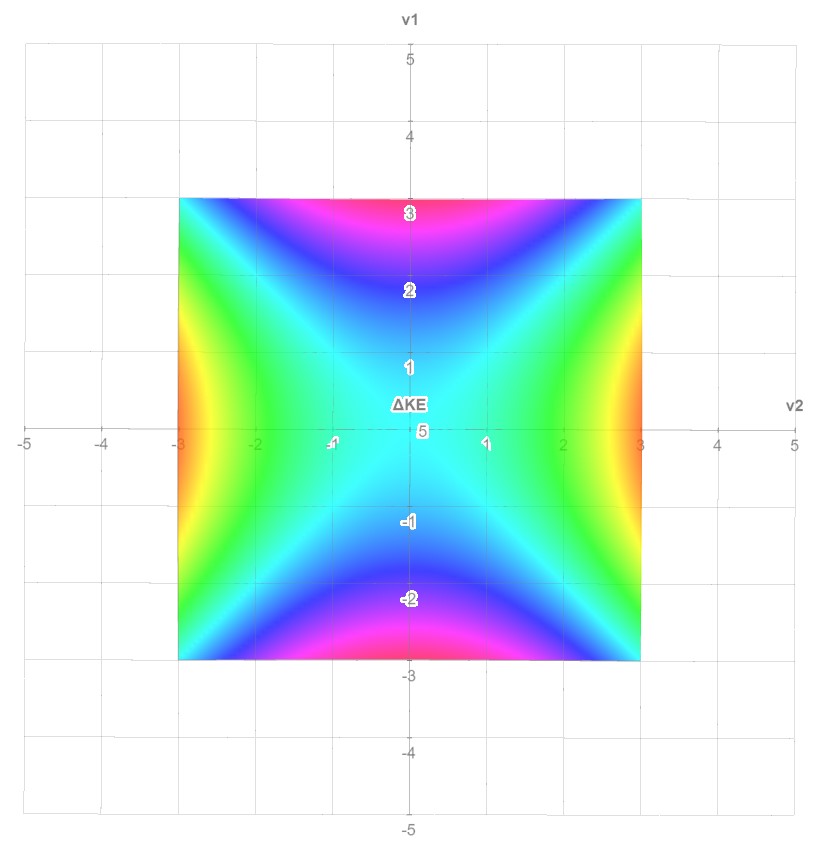
As illustrated above, for a constant change of velocity (i.e., constant \(\Delta v = v_2 - v_1\) where \(v_2 > v_1\)), the change in kinetic energy is greatest when the individual values of \(v_1\) and \(v_2\) are larger. For example, let the change in velocity be \(\Delta v = 1 {m/s}\) (assume unit mass of 1 kg). If the initial velocity is \(1 {m/s}\) and the final velocity is \(2 {m/s}\), the change in kinetic energy is \(3J\). However, if the initial velocity is \(2 {m/s}\) and the final velocity is \(3 {m/s}\), the change in kinetic energy is \(5J\). This example shows that equal changes in velocity with different starting conditions can produce different changes in kinetic energy (i.e., \(3J\) compared to \(5J\)). That is, a greater change in kinetic energy is possible, using the same change in velocity, when the change in velocity occurs at higher values. In summary, for a fixed amount of rocket fuel (i.e., fixed change in velocity, \(\Delta v\)), a greater change in overall kinetic energy of the rocket can be achieved by beginning the burn at a higher initial velocity.

---

Example

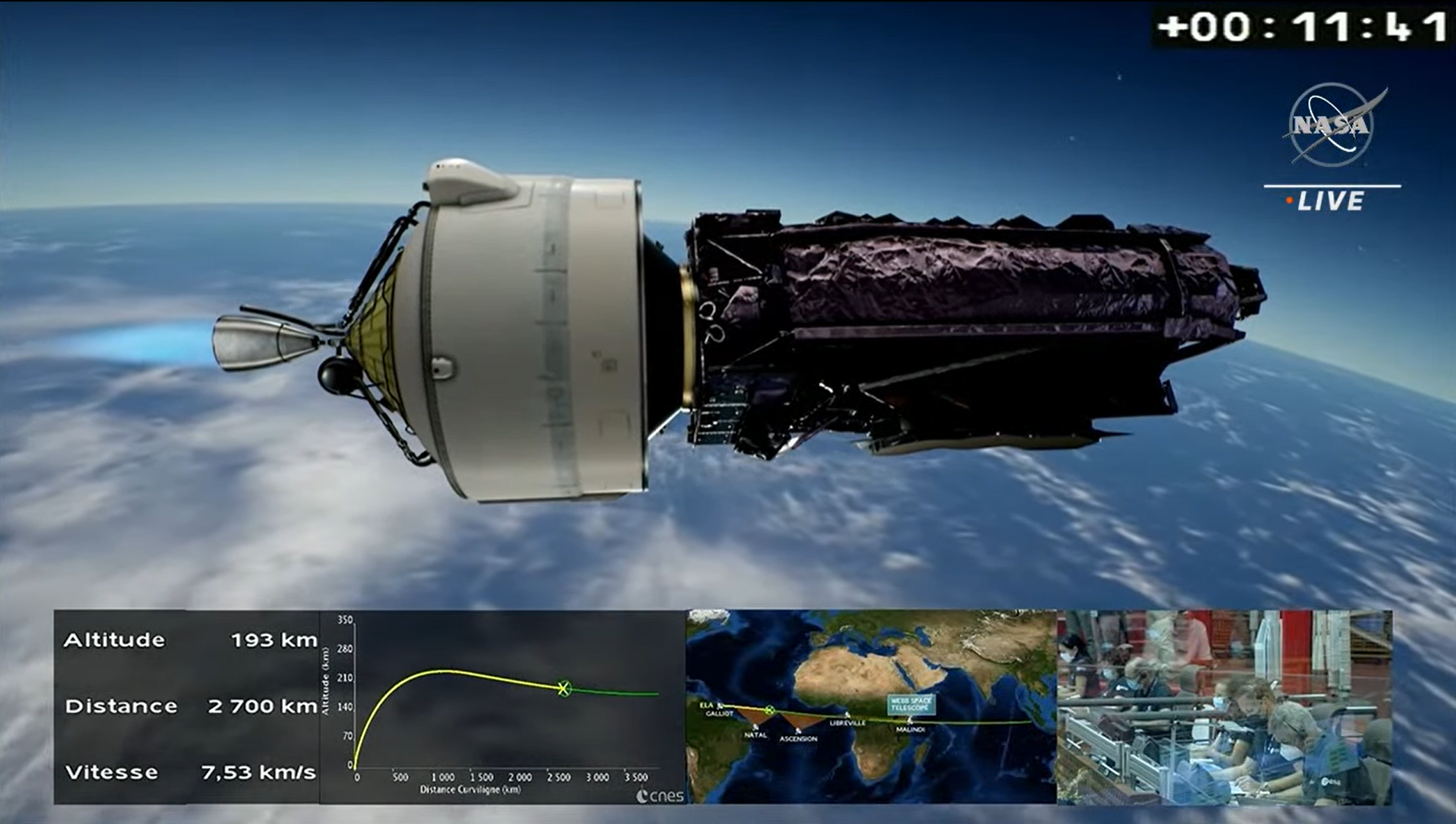
On 25 December, 2021 at 1:20pm ACDT, the James Webb Space Telescope (JWST) launched from French Guiana aboard the Ariane 5 launch vehicle. However, at about T+08m:04s, the rocket and payload began losing altitude as shown in the altitude vs. distance travelled graph belowNASA (2021) James Webb Space Telescope Launch — Official NASA Broadcast Dec 25, 2021. Available at: https://www.youtube.com/watch?v=7nT7JGZMbtM&t=6710s&ab_channel=NASA (Accessed: Jan 03, 2022).. By losing altitude, the craft traded some gravitational potential energy for some extra kinetic energy - increasing its speed. Now at a higher initial velocity than it would have been without the energy trade, the rocket began burning its engines for a specific change in velocity. The total kinetic energy increase was more efficient due to the engine burn at higher initial speed (Oberth effect). Utilising the Oberth effect, the Ariane 5 achieved such a fuel efficient payload orbit injection that the JWST now has significantly more propellant than expected to sustain its exploration mission. This extra propellant is expected to extend the lifetime of the JWST far beyond its initially expected 10 years.

Altitude versus curvilinear distance for the launch of the James Webb Space Telescope.